How to fit exponential curve?
In this Excel tutorial, you will learn how to fit an exponential curve.
Excel Functions for exponential curve fitting
Excel supplies two functions for exponential regression, namely GROWTH and LOGEST.
LOGEST is the exponential counterpart to the LINEST function described in Testing the Slope of the Regression Line. We can use the function by entering the array function =LOGEST(R1, R2, TRUE, TRUE), where R1 = the array of observed values for y (not ln y) and R2 is the array of observed values for x, and then press Ctrl-Shft-Enter.
LOGEST doesn’t supply any labels, so you will need to enter these manually. Essentially, LOGEST is simply LINEST using the mapping described above for transforming an exponent model into a linear model. For Example 1 the output for LOGEST(B6:B16, A6:A16, TRUE, TRUE) is as in below figure:
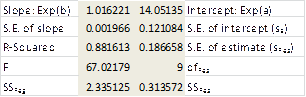
GROWTH is the exponential counterpart to the linear regression function TREND described in Method of Least Squares. For R1 = the array containing the y values of the observed data and R2 = the array containing the x values of the observed data, GROWTH(R1, R2, x) = EXP(a) * EXP(b)^x where EXP(a) and EXP(b) are as defined from the LOGEST output described above (or alternatively from the Regression data analysis). E.g., based on the data from Example 1, we have:
=GROWTH(B6:B16, A6:A16, 26) = 21.35
which is the same result we obtained earlier using the Regression data analysis tool.
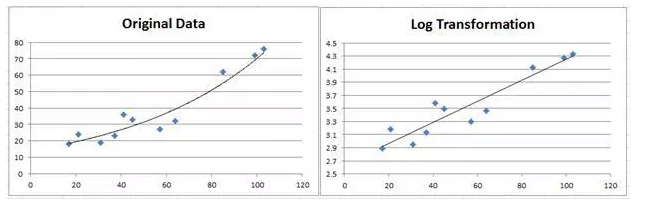
Fitting exponential functions to data
GROWTH can also be used to predict more than one value.
In this case, GROWTH(R1, R2, R3) is an array function where R1 and R2 are as described above and R3 is an array of x values. The function returns an array of predicted values for the x values in R3 based on the model determined by the values in R1 and R2.
Observation: Note that GROWTH(R1, R2, R3) = EXP(TREND(R1, R2, LN(R3)))


Leave a Reply