Howto Illustrate of the Central Limit Theorem in Excel
The Central Limit Theorem (CLT) stands as a cornerstone in the world of statistics, asserting that the distribution of sample means approximates a normal distribution, regardless of the population’s original distribution. This holds true as long as the sample size is sufficiently large and the population has a finite level of variance. Through the versatility of Excel, we can visually and practically understand this profound concept.
Step 1: Generating Random Data
Begin by creating a dataset that represents a population with a non-normal distribution. Excel offers functions like RAND(), RANDBETWEEN(), and BINOM.DIST() to generate various types of distributions. For instance, using =RAND() in cells A1 to A1000 will generate a uniform distribution of random numbers between 0 and 1.
Step 2: Sampling from the Population
Sampling is a crucial step in applying the CLT. Randomly select samples from the population data. Typically, a sample size greater than 30 is considered adequate. For example, draw 30 random numbers to form a sample and repeat this to create multiple samples.
Step 3: Calculating Sample Means
For each sample, calculate the mean using Excel’s AVERAGE() function. If your first sample occupies B1 to B30, the mean would be calculated with =AVERAGE(B1:B30).
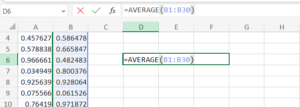
Store these means as they are central to demonstrating the CLT.
Step 4: Plotting the Distribution of Sample Means
With a substantial number of sample means, their distribution can be plotted. Excel’s histogram tool under the Insert tab is ideal for this. As per the CLT, this distribution should resemble a normal curve, which is a powerful illustration of the theorem.
Observations and Conclusions
Several key observations can be drawn from this exercise:
- Shape of Distribution: The distribution of sample means will increasingly resemble a normal distribution as the number of samples grows.
- Mean of Sample Means: This will approximate the population’s true mean, showcasing the accuracy of the CLT.
- Standard Error: The standard deviation of the sample means (standard error) will be the population’s standard deviation divided by the square root of the sample size, validating the theorem’s predictive power.
Excel not only serves as a powerful tool for statistical analysis but also becomes a medium through which the abstract becomes tangible. The CLT’s demonstration in Excel is more than a mere academic exercise; it provides practical insights into the nature of sampling and the predictability of data in the real world. As such, Excel proves to be an invaluable ally for students and professionals alike in the realm of statistics.
