How to test Statistical Significance by T-test?
A t-test is a statistical test that helps to determine if there is a significant difference between the means of two sets of data. In MS Excel, we can easily test statistical significance by using the function TTEST. Let’s first understand the parameters of this function.
Ttest function syntax
=TTEST(array1, array2, tails, type)
Array1 (Required): Range for dataset 1
Array2 (Required): Range for dataset 2
Tails (Required): This determines if it is a one-tail T-test or two tail T-test.
- 1: One tail T-test
- 2: Two tail T test
Type (Required): Type of t-test
- 1: Paired T-test, i.e. if the two data sets are related to each other
- 2: Unpaired T-test, the two samples have equal variance
- 3: Unpaired T-test , the two samples have unequal variance
T-test formula example
Example:
1. Consider the following dataset for T-test.
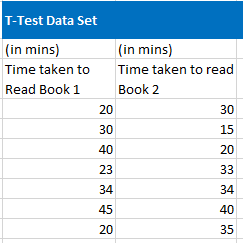
2. Select the two –datasets in array 1 and array 2.
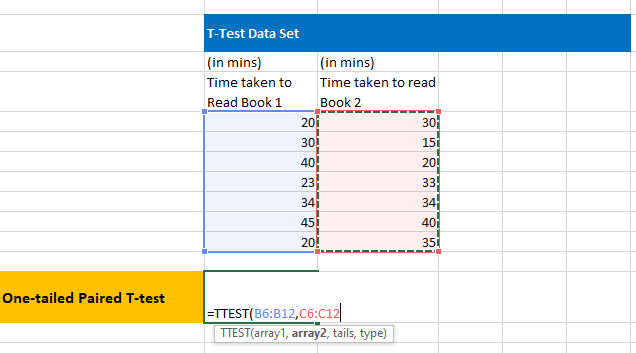
3. On an Empty Cell, write the formula to perform 1-tail Paired T test
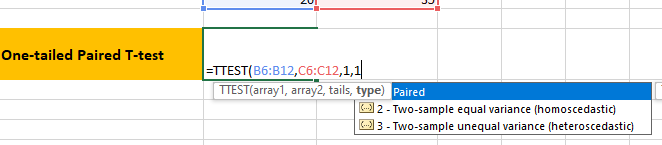
One-tailed probability obtained

4. Similarly, perform a two–tailed paired T test
![]()
Two-tailed probability obtained
![]()
Based on the obtained value you can accept or reject the null hypothesis. If the T-test gives the probability less than 0.05, then reject the null hypothesis. This means there is less than 5% probability that the null hypothesis is true.
Here, in both cases, p-value> 0.05. So, we accept the null hypothesis.


Leave a Reply