How to use Solver in Excel
The solver in Excel is part of an analysis tool known as “What-If analysis”. You can use a solver to ascertain an optimal value in one cell known as the “target cell”.
Basically, a solver is used for a group of cells that are directly or indirectly related. Constraints can also be applied to minimize the value that can be used by Solver. We will provide a step-by-step guide on how to use Solver to find a solution to a business problem.
Install, Start-up the Solver Add-in and follow the process
Before you begin, ensure that the Solver is already installed on your computer. Go to the menu bar and click on Data. The Solver is displayed on the right side under the Analysis. If you don’t see it, then Solver may not be installed.
To install the Solver tool, click the Options on the green File tab. Under the Add-Ins option, click on the Solver and then click on the Go button.
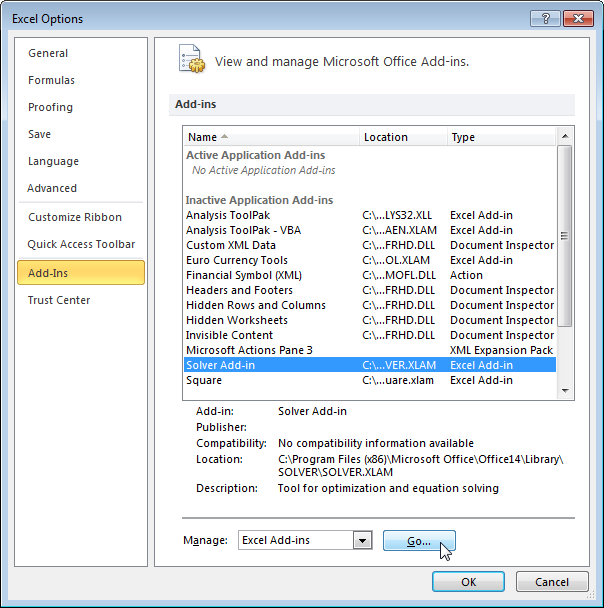
Choose the Solver Add-in.
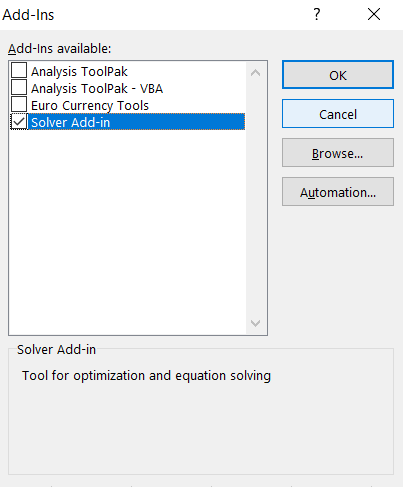
The Solver has just been installed and added to your Excel. The Solver can be located on the Data tab under the Analysis field.

After opening the Solver, a dialog box loads automatically, which allows you to specify the parameters with which you want to run the Solver.
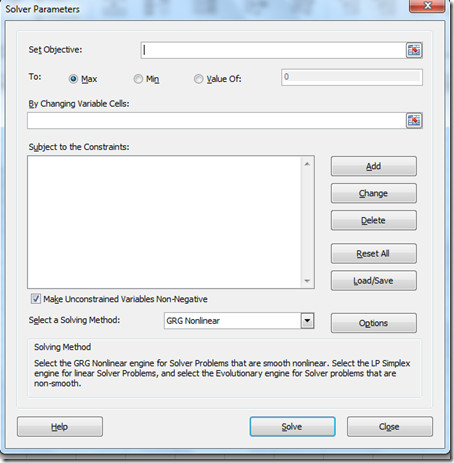
The parameters you specify will depend on the type of problem you want to solve. But the most common types of parameters are constraints, changing cells, and target cells.
Using Solver Tool in Excel
Suppose you take a bank loan to purchase UPS, furniture, computers, and other accessories needed to successfully run a cybercafé. We can make use of the PMT function to find the number of monthly installments needed to completely repay the bank.
The regular monthly expenses include maintenance, electricity, salaries, internet charges to the ISP, rent, advertisement costs, and telephone costs. The rented accommodation can take up to 24 computers, but let’s begin with 12.
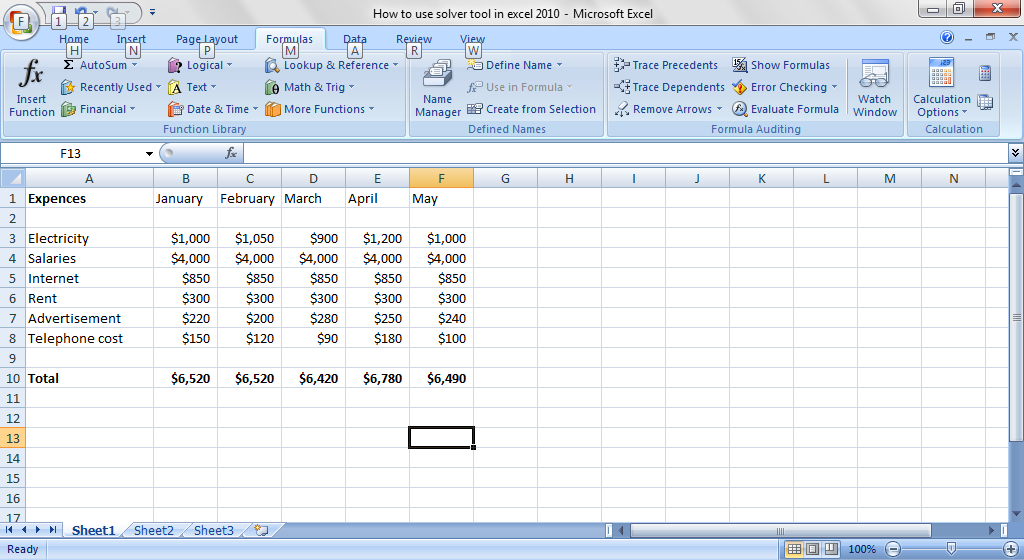
Based on the cost, the minimum amount to charge the customers can be determined. But at this point, we are not going to concern ourselves with profit. The estimates will be made for break even point (because we want to repay the bank loan before looking at profits).
Using the Solver and an analysis of the per hour rates obtainable in other cybercafés, a what-if-analysis can be done to determine what can be charged to customers.
Go to Data and select Solver. When the new window appears, select the target cell and equate its value to a certain number, like 70,000 or 100,000.
You may decide to set the lowest or highest value, but we won’t need to set this level in this example. If we are dealing with the minimization of cost here, then the maximum and minimum options will be useful.
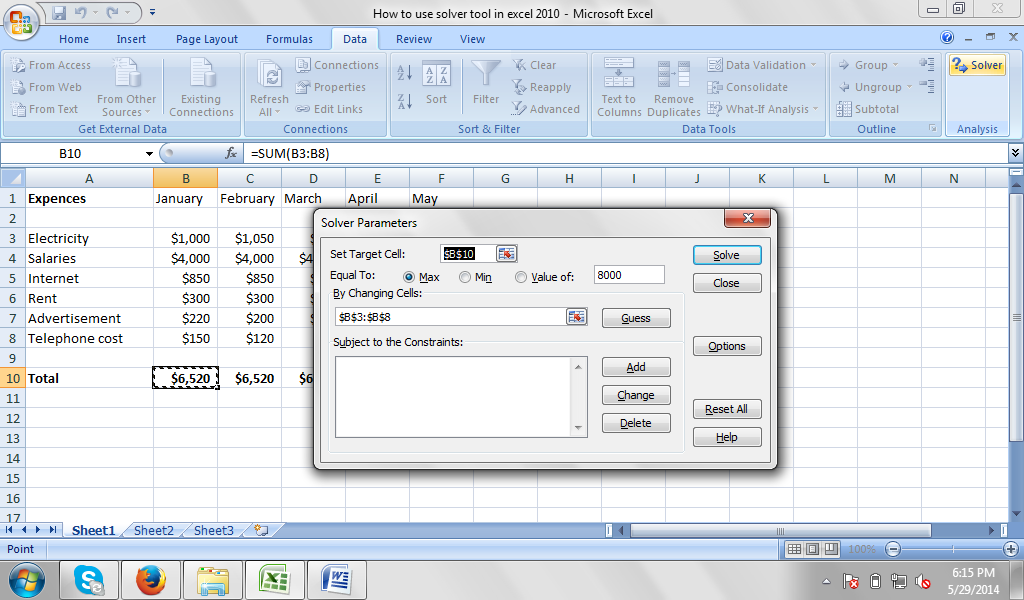
If you want, you can equally set the value to be zero (0), which will allow you to establish the break even point where the monthly earnings will be equal to the monthly expenditures.
The final step is to determine the cells that will affect the target cell. Determine the constraints, like the minimum and maximum hours of work and the minimum and maximum numbers of computers.
It is important to make sure that the number of computers is a whole number. You can’t have 2.4 computers because it will be difficult to analyze the data.
We also need to determine the lowest and highest amount that can be charged per hour for the cybercafé as determined by the research from other cybercafés. When this is done, input the necessary figures and make use of the Autosum features.
You can now use the saved data to manage your expenses and income until you approach breakeven for the loan collected.
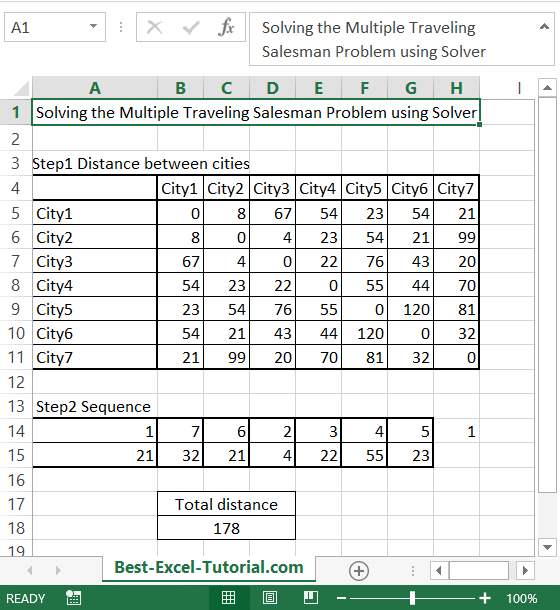
Solving the Multiple Traveling Salesman Problem using Solver
Let’s calculate the Multiple Travelling Problem. This is a well-known mathematical problem to solve, which requires complicated and time consuming calculations.
The clue to the Multiple Traveling Salesman Problem is to find the shortest possible path for deliveries to many places. The Salesman needs to visit each city only once before going back home.
The Solver will calculate the proper order between cities. This is very needed in modern times when many companies struggle to use their resources in the most efficient way.
To solve the traveling salesman problem, you need to prepare a matrix of data. This is the distance between the cities the salesman needs to visit before going back to his home city. Each city needs to be visited only once.
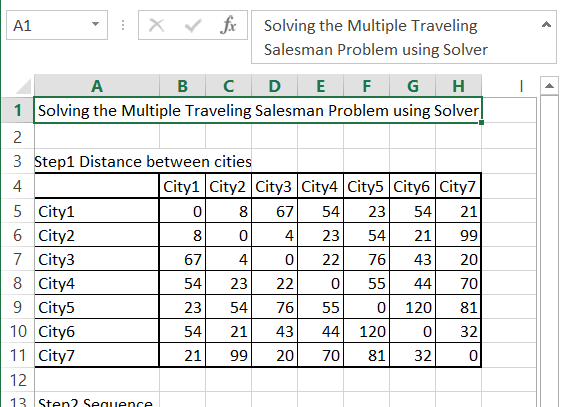
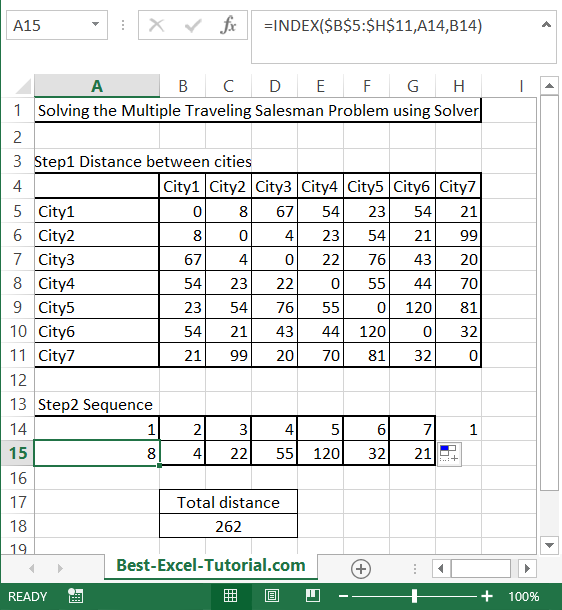
Then, in the next step, prepare the random order of cities. In the eight column, put in the starting city using the =A14 formula. In the column below, put the distance between the cities using the INDEX function. The formula is =INDEX($B$5:$H$11,A14,B14)
Calculate the total distance using the simple SUM function. Formula here is =SUM(A15:G15)
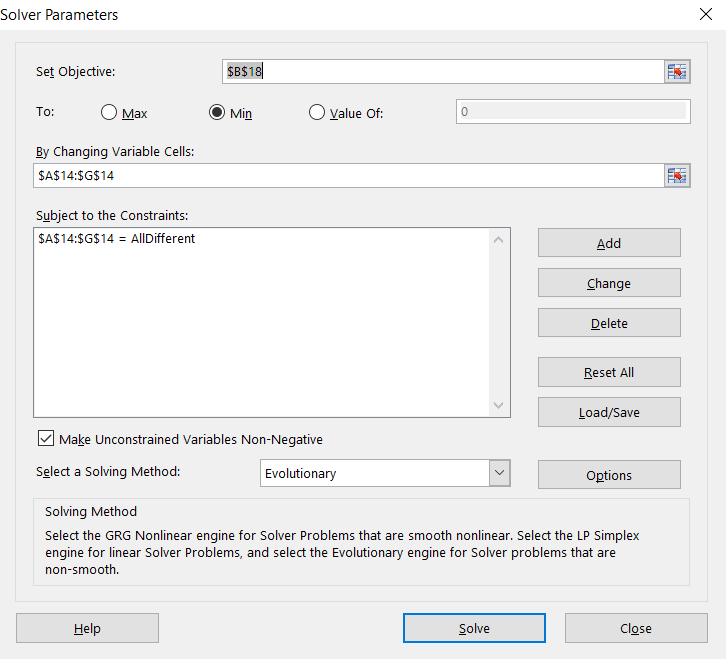
Then go to Solver and fill it in as follows:
- Set Objective – minimize (Min) the Total distance ($B$18).
- By changing variable cells – Order of cities ($A$14:$G$14).
- Subject to the Constraints – add that all cities needs to be different since each city needs to be visited only once ($A$14:$G$14 = AllDifferent).
- Select a Solving Method – to get better solution use Evolutionary.
This is how to solve the Multiple Travelling Problem by finding the shortest path. The Solver gives you a much better solution than your random one.
The Solver is a powerful tool that can be used to find optimal solutions to a variety of problems.


Leave a Reply