How to Use NPER Function in Excel
In this lesson, you can learn how to use NPER function in Excel.
The NPER function is similar to the Future Value and Present Value functions. The difference, however, is that the NPER formula will return the investment amount using periodic, constant payments and interest. The NPER function calculates the number of periods for an investment or loan, assuming constant payments at regular intervals and a constant interest rate.
Syntax for the Nper function
Syntax is:
- Rate is the interest rate for each period.
- PMT is the fixed payment made in each period.
- PV is the present value of the investment or loan.
- FV FV is the future value of the investment or loan.
- Type is the timing of payment during the period. 0 means payments are made at the end of each period and 1 means payments are made at the beginning of each period.
The rate parameter should be provided for the payment period, ie if the interest rate is given annually and monthly payments are then divide the interest rate for 12 months.
In the case of an investment, PMT, PV, and FV are negative and positive respectively. For a loan, PMT is negative, PV is positive and FV is negative, if only partial repayment is made.
How NPER works
NPER works by using a trial and error method to find the number of periods required to pay off the loan. It starts with the guess value you provide and then iteratively increases or decreases the number of periods until the present value reaches the future value.
The optional guess value can be helpful if you have a good estimate of the number of periods required. If you don’t provide a guess value, Excel will use a default value of 10.
Nper function examples
Here are some examples of how to use NPER:
Basic calculation of NPER
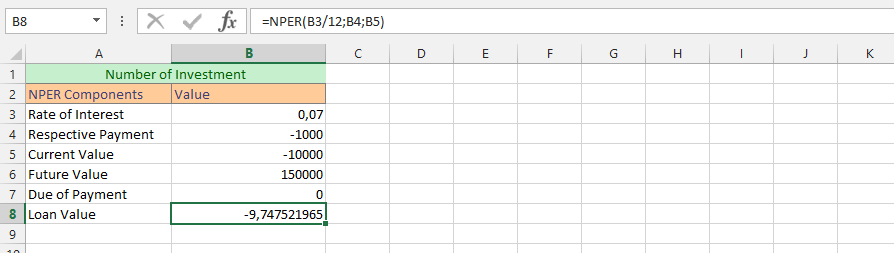
How many payments you must pay to reach a value of 1 000 000 $ for investment with an annual interest rate of 10%? You pay monthly payments in the amount of 1 000 $, having already set aside 150 000 $. You pay at the end of each period (month).
Formula is =NPER(0.10/12,-1000,-150000,1000000,0)
Answer: Result is 171,43 what means, that you need 172 payments to reach 1 000 000$
Explanation:
- 0.10/12 – rate is 10% what must be divided by count of months
- -1000 – monthly payment (with minus because you have to pay)
- -150000 – your current cash (with minus because you pay)
- 1000000 – your future value (without minus because it’s your cash)
- 0 – because you pay at the end of the period
How much do you need to pay off your loan?
To find out how many payments are needed to pay off a $100,000 loan with a monthly installment of $700 (principal and interest) and an annual interest rate of 8%, the corrected formula is:
=NPER(0.08/12, -700, 100000, 0, 0)
Answer: The result is approximately 187.89, meaning that you would need 188 payments to pay off this loan.
Explanation:
- 0.08/12 represents the monthly interest rate, derived by dividing the annual rate by 12.
- -700 is the monthly payment, negative because it’s an outflow.
- 100000 is the present loan amount, positive because it reflects the borrower’s liability.
- 0 is the future value, indicating the goal is to fully repay the loan.
- 0 signifies payments are made at the end of each period.
NPER when you pay at the beginning of the month
You can also find the number of payments needed to reach a future value, such as in the case of saving $18,000 with monthly payments of $300 and an annual interest rate of 3.5%, with payments made at the beginning of each month. The formula for this scenario would be =NPER(0.035/12, -300, 0, 18000, 1). The result shows that 56 months of payments would be needed to reach the future value.
Answer: Result is 55,22 what means, that you need 56 months to reach $18 000.
Explanation:
- 0.035/12 – rate is 3.5% what must be divided by count of months
- -300 – monthly payment (with minus because you have to pay)
- 0 – your current cash
- 18 000 – your future value (without minus because it’s your cash)
- 1 – because you pay at the beginning of the period

Leave a Reply