How to use the integral function?
Integration is part of the important concepts that are associated with mathematics and is part of the main operations in calculus. It has to be given the function f of a variable x that is real, as well as the interval which is a, b, of that real line, and this is the definite integral:
![]()
This has been informally defined as the signed area of a region that is in the x/y-plane and has its boundary defined by a graph of f, the x-axis, as well as vertical lines x that is a, and x that is equal to b. The term known as integral could also refer to the related notion of antiderivative, which is a function F whose derivative is the function that is given. In such a case, an indefinite integral is defined and also written like this:
![]()
You are going to work with the integral of a simple calculation by following the simple steps below.
Data Layout
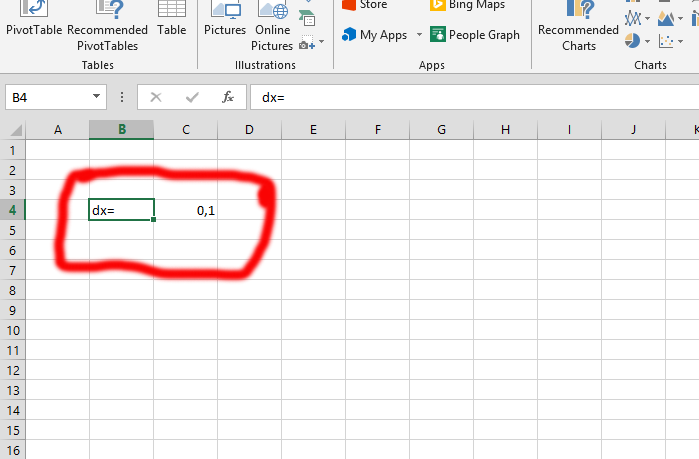
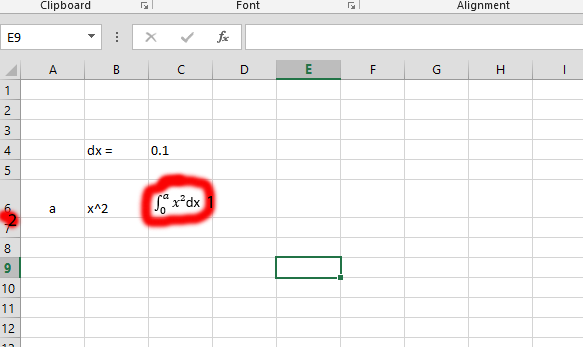
You should decide the dx value, which is 0,1. This is shown in the picture above.
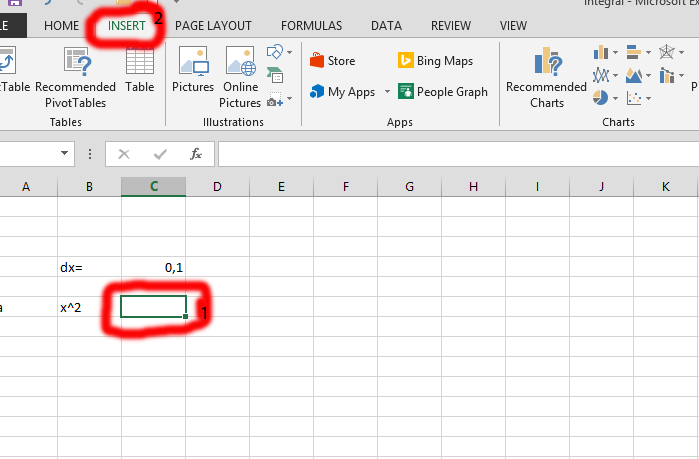
Click on the column that is beside the x^2, and labeled as number 1. Click on the Insert tab, the one labeled as number 2.
Click on the equation, which is marked in red. Do not click on the arrow, just on the equation itself.
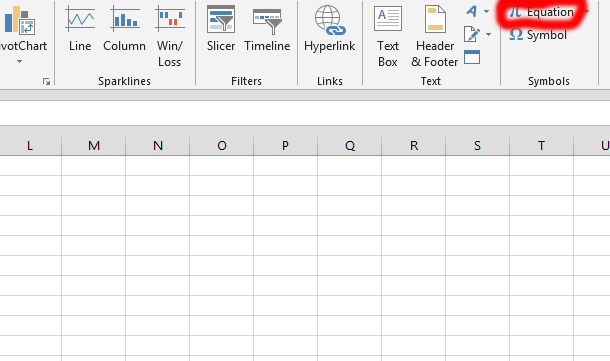
Click on the integral (labeled number 1) that shows up once you have clicked on the equation in the previous step. Then click on the kind of integral you would like. In this case, the one labeled number 2 is chosen.
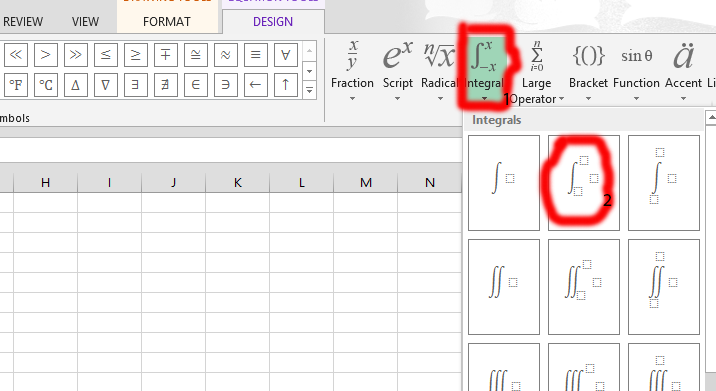
Place the values that are relevant to the integral function. As you can see, the one marked in red and labeled as number 1 is going to have a detail of your choice. On top of the f there is a, while at the end there is a 0, and in the middle there is an x. You should click on the line (where number 2 is marked) and expand the whole row to fit the integral equation that has been inserted.
Tip: you should type in the x2 (marked with the number 1), using an insert symbol (which is in the insert tab).
Integral Calculation
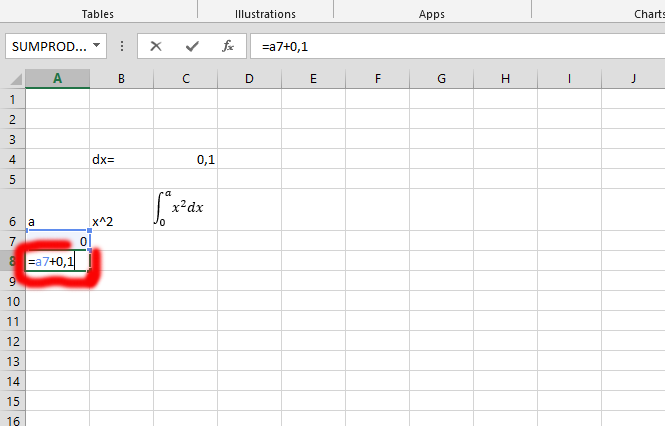
Add 0 (in this case in a7) with the 0,1 – the dx.
Information: If you see any error in calculating, you should change from 0,1 to 0.1 to continue.
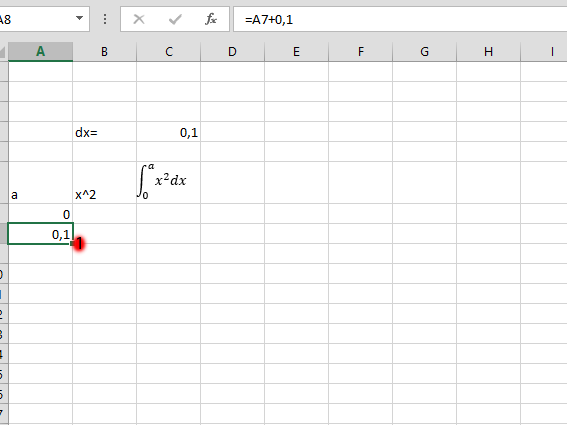
Click on the small square beside the number 1, using your mouse. Drag it down to the end, as you wish. In this case, it is dragged to a20.
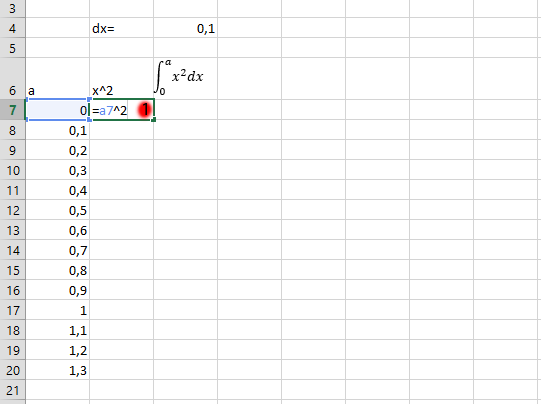
Click on the column in the row of the ^2, and add the content in “a” row to multiply with ^2. Repeat the step 2 – 2 with the A row, as it is in this case. Check the picture for clarification.
Type in the columns that are relevant to the integral you are calculating. You would see the marked columns, as well as some added numbers.
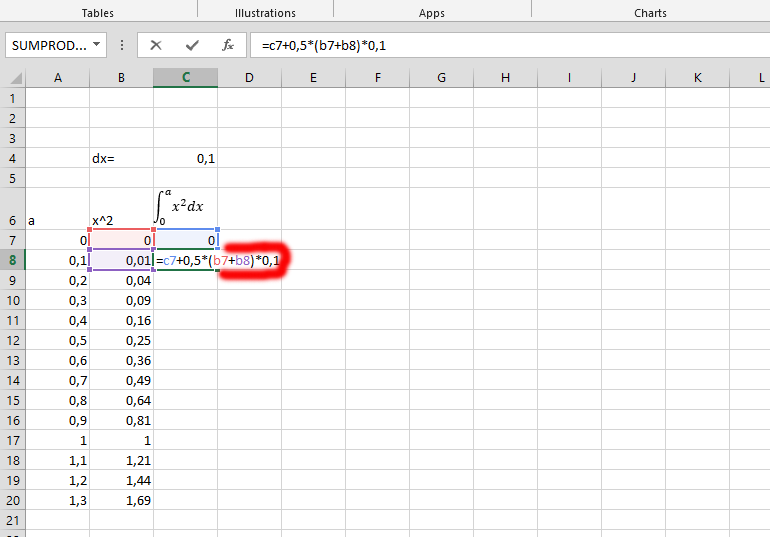
Click on the integral you have just calculated, and now click on the small square that is in the marked area and on the left side of the one labeled number 1, and drag it down to save yourself the stress of calculating one after the other.
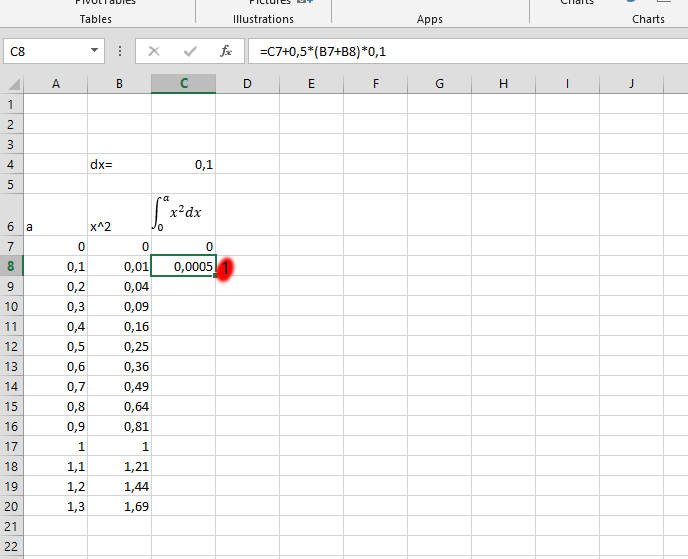
Design (Optional)
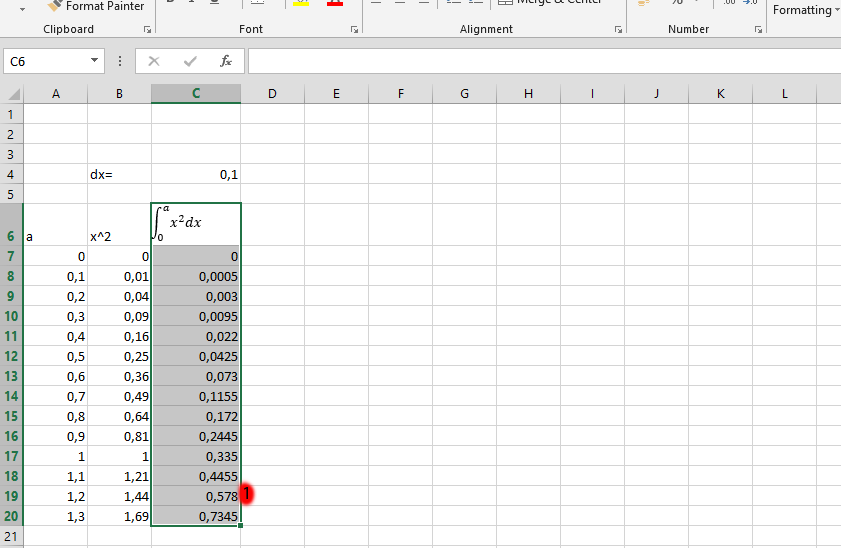
Mark the rows you would like to display in a specific design.
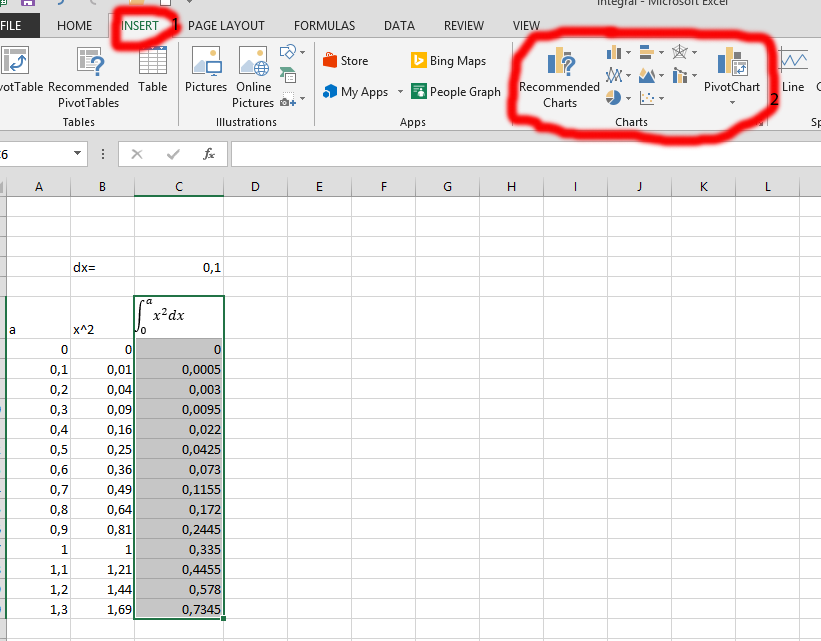
Click on the INSERT tab, the one labeled as number 1, and then choose the type of chart you would like to display, which is labeled as number 2.
Choose the design you would prefer for your integral chart.
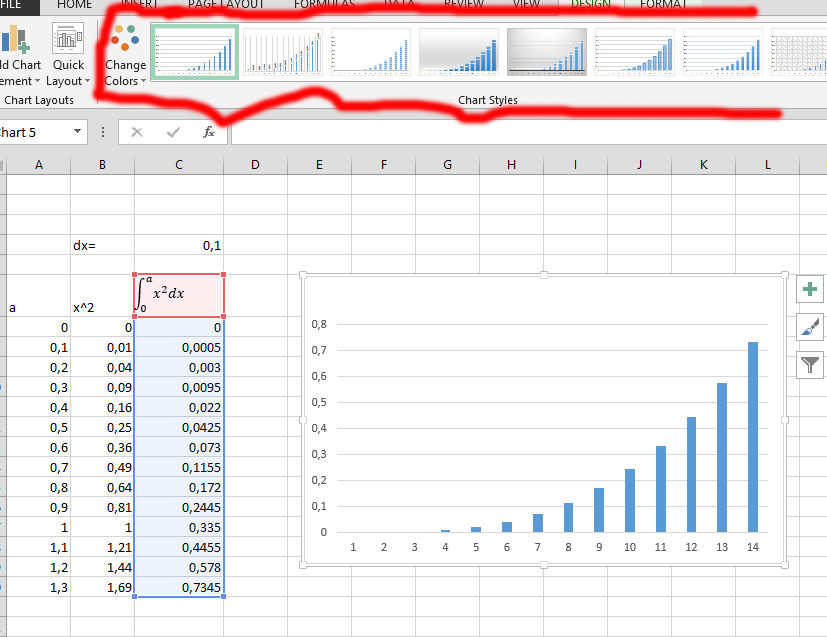
Insert the column chart of your integral of a function and write the title you would like to give the chart.
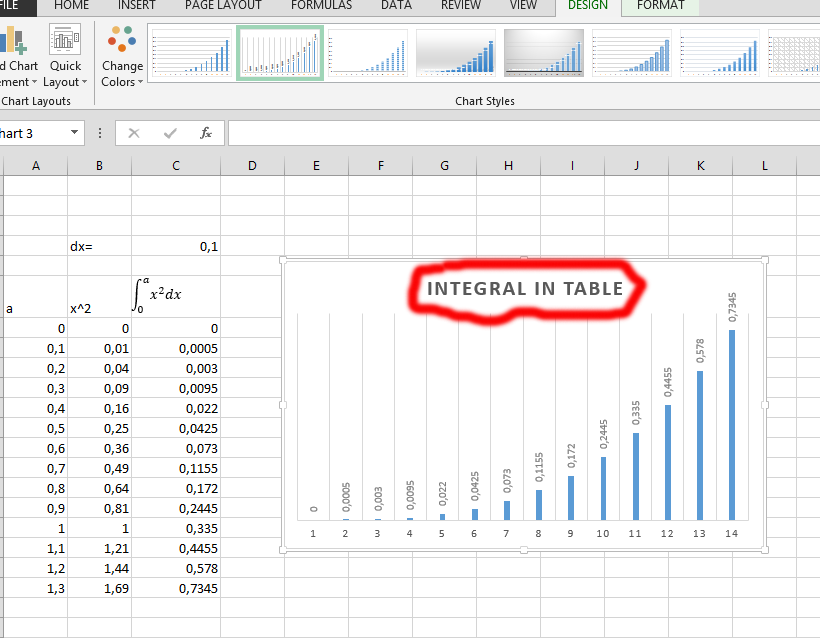
The chart is ready.

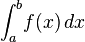

Holdcraft
This post is a great read! Your points are extremely well-articulated and the writing is very engaging. Keep up the amazing work!