The Newton-Raphson method is a numerical method used to find the roots of an equation, i.e., the values of x that make the equation equal to zero. It is a powerful tool for solving complex non-linear equations, and it can be implemented in Excel using a combination of the "Goal Seek" function and a user-defined function.
The Newton-Raphson method is based on the idea of iteratively improving an estimate of the root, based on the tangent line to the curve of the equation at the current estimate. The method starts with an initial guess for the root, and then calculates a new estimate.
Follow the steps below to learn how to use Newton Raphson Method in Excel.
Newton Raphson Method to solve the equation
We are going to use the Newton Method to solve the equation x^2=5
First, you need to label the column like this.
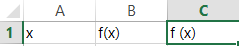
Note: Argument (x) is required for a column for function evaluations (f(x)), and a column for slope (f\’(x)).
Preparing Newton's method calculator
Fill in the value in (x).
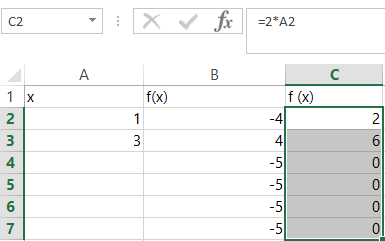
In column B write the formula =A2^2-5 and in column C write the formula 2*A2
In column A cell A3 enter the formula =A2-B2/C2. Select cell B2, move the cursor to the bottom right, a black plus sign will appear. Drag the black plus sign to cell B7.
Repeat with cell C2.
Repeat with cell A1. That's it. You have now learned how to use the Newton Method in Excel.
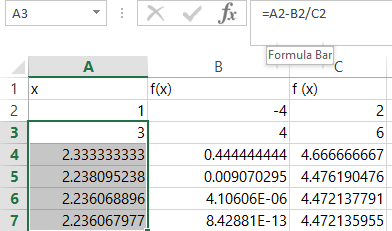
Note that once the value of x no longer varies from row to row and f(x) is small (close to zero), you have the solution (assuming the process has converged).
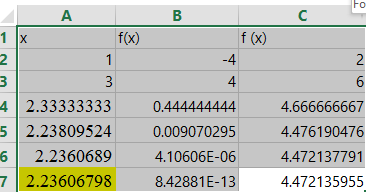
Note: Answer is shaded in yellow.
Preparing Newton's method VBA calculator
You can also use VBA code to create a user-defined function that implements the Newton-Raphson formula. This function will take two arguments: the current estimate of the root, and the equation being solved.
To create the user-defined function, you will need to use the VBA (Visual Basic for Applications) programming language. You can access the VBA editor in Excel by pressing the "Alt + F11" keys.
In the VBA editor, go to the "Insert" menu and select "Module." This will create a new module where you can write the user-defined function.
The following is an example of a VBA function that implements the Newton-Raphson method:
Function NewtonRaphson(x0 As Double, eq As Range) As Double
Dim f As Double
Dim df As Double
f = eq.Cells(1).Value
df = Application.Evaluate("=D(" & eq.Address & "," & eq.Cells(1).Address & ")")
NewtonRaphson = x0 - f / df
End Function
In this function, x0 is the current estimate of the root, and eq is the equation being solved, represented as a cell reference in Excel. The function first calculates the value of the equation, f, and its derivative, df, using the Application.Evaluate method.
The derivative of the equation is calculated using the D function, which is a built-in function in Excel that calculates the numerical derivative of a function. The Address property of the eq range is used to pass the cell reference of the equation to the D function.
Finally, the function returns the updated estimate of the root, x0 - f / df, using the Newton-Raphson formula.
The last step is to use the "Goal Seek" function to iteratively improve the estimate of the root, based on the output of the user-defined function.
To do this, go to the "Data" tab in Excel and select "What-If Analysis" and then "Goal Seek." In the "Set cell" field, enter the cell reference for the equation that you want to solve. In the "To value" field, enter 0, since you are trying to find the roots of the equation. In the "By changing cell" field, enter the cell reference for the current estimate of the root.
Finally, click the "OK" button to start the iteration process. The "Goal Seek" function will use the user-defined function to calculate a new estimate of the root, and repeat the process until the equation equals 0 within a specified tolerance.
Note that the "Goal Seek" function may not always converge to the root of the equation, depending on the initial guess and the nature of the equation. In these cases, you may need to modify the initial guess and try the process again.