In this lesson, you will learn how to calculate variance in Excel.
Smple Variance vs. Population Variance
The syntax of variance functions
Examples of the VAR function in Excel
How to calculate the variance between two numbers
What is the variance
Variance is the primary measure of the variability of the results observed.
Variance tells you how far the spread is in the set of measurements. In other words, remember the basic rule of variance. Regardless of whether the scores are centered around the mean or there are large differences between the mean and the individual scores. The higher the variance, the more the values vary.
If the values of the studied random variables differ significantly from the mean value, the variance has a much greater value. The variance would be smaller if the values of the test variables were concentrated around the expected value.
Therefore, variance is considered to be a measure of the spread of the value of a random variable around the mean. The more values of a variable are clustered around the expected value, the smaller the variance is expected to be.
Variance is always positive (except for the variance of the constant, where the variance is zero).
The variance of the numbers x1, x2, ..., xn is the arithmetic mean of the squares of deviations from their arithmetic mean. Variance is the squared value of the standard deviation.
Let's see a mathematical example of the variance equation for a better understanding.
Based on the given number, I calculated the mean first.
Then they calculated the variance in the single equation with a result of 6.5.
Variance in Excel
There are 3 basic functions which you can use to calculate variance in Excel:
- VAR: common function which calculates variance in every version of Excel. However, since the Excel 2010 version, this function has started to be improved and replaced by VAR.S and VAR.P. Although this feature is still available.
- VAR.S: calculates the sample variance of a supplied set of values. This is a new function in Excel 2010, and it's not working in earlier versions of Excel.
- VAR.P: calculates the sample variance of a whole population of values. This is a new function in Excel 2010, and it's not working in earlier versions of Excel.
With the VAR and VAR.S functions, you can calculate the variance for a sample of values. To calculate the variance for the entire population of values, just use the VAR.P function.
Sample Variance vs. Population Variance
Perhaps you are asking yourself this question. Should I calculate the population or variance of the sample? A simple explanation is to check if you have data for all of your observations (whole population) or just for some of them (sample).
The population variance refers to the calculated value of the variance from the population data. Sample variance is the calculated variance from the sample data.
For this reason, the denominator value in the variance formula is n-1 (degrees of freedom) for the sample data and n (sample size n) for the given populations.
The value of variance calculated from the sample data is higher than the value that can be obtained from the population. The logic behind this is to compensate for our lack of information on population data.
The value of the population variance calculated with the functions VARIANCE.S and VARIANCE is always greater than VARIANCE.P.
The syntax of variance functions
=VAR(number1,[number2],...])
=VAR.S(number1,[number2],...])
=VAR.P(number1,[number2],...])
=VARA(number1,[number2],...])
=VARPA(number1,[number2],...])
Examples of the VAR function in Excel
The simplest syntax of variance
As an argument to the function, you can just use numbers.
=VAR(2,3,4,5,6,7,8,125)
Cells as arguments in the formula
Arguments could also be cells where you have some numbers.
=VAR(A2,A3,A4,A5)
Range of cells as arguments in the formula
You can also use a range of cells.
=VAR(A2:A10,B4:C10)
Combination of the previous examples in a single formula
It is not a problem to use every kind of argument mentioned in one formula.
=VAR(A2:A10,B4,5,7)
The syntax of VAR.S (function of sample variance), VAR.P (function of variance of population) is the same as VAR.
Variance of the sample
How to calculate sample variance using VAR.S function?
This example is for sample calculations.
Data sampling is common because getting population-wide data is difficult, costly, and often not even possible. Examples of data based on data samples are:
- Based on the data of one team, you want to examine the data of the entire company.
- By measuring the height of students of one class, you want to show the data of the students of the entire school.
To calculate a variance of a sample you need to use VAR.S function.
The VAR.S function is used to calculate the variance of a sample.
The syntax for the VAR.S function: =VAR.S(value1, value2,…)
The formula in my case is: =VAR.S(A1:A10)
How to calculate sample variance for boolean and text values?
You already know how to calculate the variance for a data sample. In further considerations, we go into more and more advanced cases.
Take into account that the previous calculations only considered one scenario. In the earlier cases, we assumed that the data table only contained numbers.
If data other than numbers were to appear, the previously discussed functions will simply bypass them.
Let's calculate the variance for a data that contains not only numbers, but also logical and text values.
Use the VARA function to calculate the variance for logical and text data.
VARA function syntax:
=VARA(number1,[number2],...])
The difference between VAR.S and VARA is that VAR.S bypasses data that is not numbers. For the VARA function:
- TRUE is counted as 1
- FALSE equals 0
- TEXT is 0
The formula of the vara function in my case is =VARA(A1:A10).
How to calculate sample variance using the Data Analysis Toolpak Add-In?
There is also a way to calculate the sample validation without using an Excel formula. Instead of the Var.S formula, you will use an Excel add-in.
First, you need to make sure your Data Analysis Toolpak Add-In is installed. Here is the lesson on how to install the Data Analysis Toolpak Add-In.
Navigate to the Data Tab on the Ribbon. Click the Data Analysis button.
A new window appears. Choose Descriptive Statistics and click OK.
Enter the proper parameters:
- Input Range: range of your data ($A$1:$C$10 in my example)
- Labels in first row: there are no labels in my data table.
- Output Range: choose where you want to get your variance calculated (I chose the same Sheet $G$1:$T$18)
- Summary statistics: make sure it is checked
And this is how you can see my Statistics summary. Sample variance is calculated in row 8.
Variance of the population
How to calculate population variance using VAR.P function?
This example is for variance population calculations.
To calculate a variance of a population you need to use VAR.P function.
The VAR.P function is used to calculate the variance of a population.
The syntax for the var.s function: =VAR.P(value1, value2,…)
The formula in my case is: =VAR.P(A1:A10)
How to calculate population variance for boolean and text values?
Let's calculate the population variance for data that contains not only numbers but also logical and textual values.
Use the VARPA function to calculate the population variance of the logical and text data.
VARPA function syntax:
= VARPA (number1, [number2], ...])
The difference between VAR.P and VARPA is the same as that between VAR.S and VARA. Similarly, VAR.P omits data that is not numbers.
For VARPA functions also:
- TRUE is counted as 1
- FALSE equals 0
- TEXT is 0
The VARPA formula is used to calculate population variance in logical and textual data.
The formula for the VARPA function in my case is =VARPA(A1:A10).
How to calculate the variance between two numbers
Variance can also be understood as percentage difference.
To calculate the variance of two numbers, you can use one of the following formulas:
Variance between two numbers = (number 1 - number 2) / number 2
Variance between two numbers = (number 1 / number 2) - 1
In the example you can see in the example below, I found the percentage difference between the numbers 5 and 4.
In the first method, I used the formula =(C2-C3)/C3
The variance formula that I used in Method 2 is =C2/C3-1
In both cases the result is the same, proving that both methods are valid.
Variance between two numbers:
- is greater than zero when the number 1 is greater than the number 2
- is zero when the numbers are equal
- is less than zero in the case when the number 2 is greater than the number 1.
Further reading: Statistical process control chart
How to insert variance graph
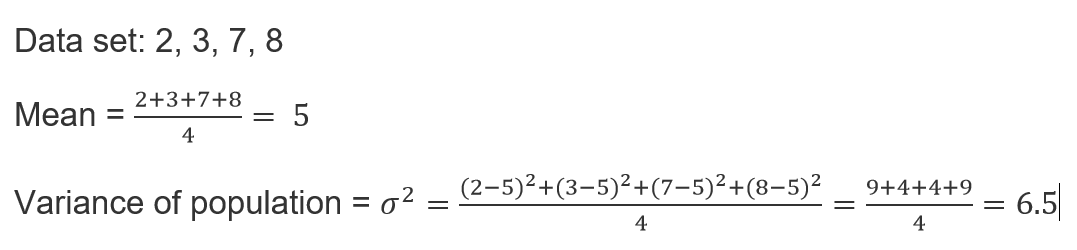
Variance of uniform distribution How to calculate covariance? Calculating forecast accuracy and precision How to calculate a variance estimator? How to calculate variance in Pandas